Hogyan találja meg a központi szöget egy szektor területe és sugara alapján?

Tartalomjegyzék:

A középső szög meghatározása a szektorterületről

Videó: Hogyan találja meg a központi szöget egy szektor területe és sugara alapján?

2024 Szerző: Miles Stephen | [email protected]. Utoljára módosítva: 2024-01-18 08:16

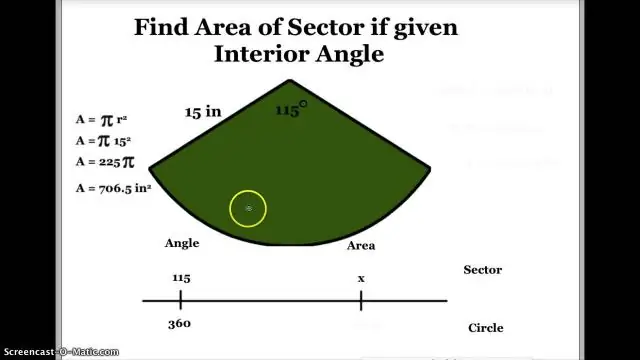
A középső szög meghatározása a szektorterületről

(πr²) × ( központi szög fokban ÷ 360 fokban) = ágazati területen . Ha a központi szög radiánban mérik, a képlet helyett a következő lesz:
ágazati területen = r² × ( központi szög radiánban ÷ 2).
(θ ÷ 360 fok) × πr².
(52,3 ÷ 100π) × 360.
(52.3 ÷ 314) × 360.

Ilyen módon hogyan találja meg a középponti szöget a sugár alapján?

megtalálja az Középső szög az Ívhossztól és Sugár Használhatja a sugár a körből és az ív hosszából megtalálja az központi szög . Hívja a mértékét a központi szög θ. Ekkor: θ = s ÷ r, ahol s az ívhossz és r a sugár.

A fentieken kívül hogyan találja meg egy szektor középponti szögét? A középső szög meghatározása Tól Ágazat Terület Más szóval: (πr²) × ( központi szög fokban ÷ 360 fokban) = ágazat terület. Ha a központi szög radiánban mérik, a képlet helyette a következő lesz: ágazat terület = r² × ( központi szög radiánban ÷ 2).

A fentieken kívül mekkora egy szektor területe?

Az egy szektor területe L-ben kifejezve a teljes összeg szorzásával kaphatjuk meg terület πr² L arányával a teljes kerülethez 2πr.

Mi a kerület képlete?

Az a kerületének kiszámításához kör , használja a C = πd képletet, ahol "C" a kerület, "d" az átmérő, π pedig 3,14. Ha az átmérő helyett a sugár van, szorozza meg 2-vel, hogy megkapja az átmérőt. Használhatja az a kerületének képletét is kör sugarat használva, ami C = 2πr.

Ajánlott:

Hogyan találja meg egy vektor komponens alakját a nagyság és a szög alapján?

VIDEÓ Ezt figyelembe véve 0 egységvektor? A egységvektor egy vektor amelynek nagysága 1. A jelölés annak normáját vagy nagyságát jelenti vektor v. Az alapvető egységvektorok i = (1, 0 ) és j = ( 0 , 1), amelyek 1 hosszúságúak, és irányuk a pozitív x, illetve az y tengely mentén van.

Hogyan találja meg az ív hosszát és a szektor területét?

A főív által bezárt középső szög mérete nagyobb, mint 180°. Az ívhossz képlet a körív hosszának meghatározására szolgál; l=rθ l = r θ, ahol θ radiánban van megadva. A szektor területe A=12θr2 A = 1 2 θ r 2, ahol θ radiánban van megadva

Hogyan találja meg a molaritást az abszorbancia alapján?

Az egyenletnek y=mx + b alakban kell lennie. Tehát ha kivonja az y metszőpontját az abszorbanciából, és elosztja a meredekséggel, akkor megtalálja a minta koncentrációját