Videó: Hogyan használja a 68 95 99 szabályt?
2024 Szerző: Miles Stephen | [email protected]. Utoljára módosítva: 2023-12-15 23:37
A statisztikákban a 68 – 95 – 99,7 szabály , más néven empirikus szabály , egy gyorsírás használt megjegyezni azoknak az értékeknek a százalékos arányát, amelyek az átlag körüli sávon belül helyezkednek el normál eloszlásban, két, négy és hat szórással; pontosabban az értékek 68,27%-a, 95,45%-a és 99,73%-a hazudik
Ebben a tekintetben mi a 95 százalékos szabály?
Az empirikus szabály kimondja, hogy normál eloszlás esetén szinte az összes adat az átlag három szórása közé esik. 95 %-a két szórásra esik. 99,7%-a három szórásra esik.
Tudja azt is, mi a 68% 95% és 99,7% konfidencia intervallum a minta átlagához? Mivel 95 Az értékek %-a két szórásra esik a átlagos szerint a 68 - 95 - 99.7 Szabály: egyszerűen adjon hozzá és vonjon ki két szórást a átlagos annak érdekében, hogy megszerezzék a 95 % megbízhatósági intervallum . Szerint a 68 - 95 - 99.7 Szabály: ➢ Az 68 % megbízhatósági intervallum ezért példa 78 és 82 között van.
Azt is tudni kell, hogy miért 68 százalékos a szórás?
Ahogy mások mondták, ez a számítás eredménye, hogy ez a képlet -1/2 szigmától 1/2 szigmáig terjedő integrálként számolt (1 szigma = 1) szórás ) 0,68-as görbe alatti területet eredményez, ahol a -végtelen és +végtelen közötti integrálként számolt teljes terület 1, így azt kapjuk 68 % for egy szabvány
Mi az a 95 százalékos konfidencia intervallum?
A 95 % megbízhatósági intervallum értéktartomány, amely lehet 95 % bizonyos tartalmazza a népesség valódi átlagát. A bal oldali kis mintával a 95 % megbízhatósági intervallum hasonló az adatok tartományához.
Ajánlott:
Hogyan használja a szorzat és hányados szabályt?
A szorzatszabály azt mondja, hogy két függvény szorzatának deriváltja az első függvény szorzata a második függvény deriváltjával, plusz a második függvény szorzata az első függvény deriváltjával. A Termékszabályt akkor kell használni, amikor két függvény hányadosának deriváltját kell felvenni
Hogyan old meg egy kitevő szabályt?
Csak a negatív kitevőket mozgassa. Termelési szabály: am ∙ an = am + n, ez azt mondja, hogy két kitevő szorzásához ugyanazzal az alappal, megtartjuk az alapot, és összeadjuk a hatványokat., ez azt mondja, hogy ha két kitevőt ugyanazzal az alappal osztunk fel, akkor megtartjuk az alapot és vonjuk le a hatványokat
Hogyan használja a jobbkéz szabályt kereszttermékekhez?
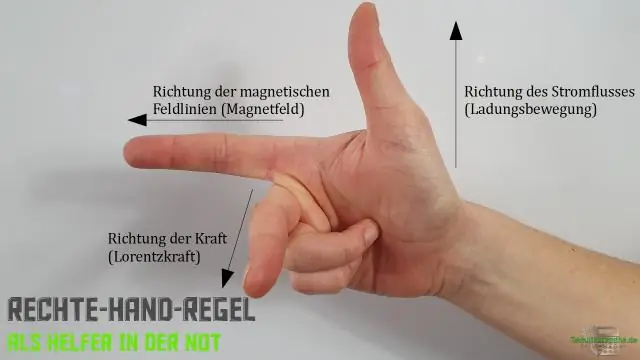
A jobbkéz szabály kimondja, hogy a vektorok keresztszorzatának orientációját a jobb kéz egymáshoz helyezése, a jobb kéz lelapítása, az ujjak irányába történő kinyújtása, majd az ujjak a szög által alkotott irányba történő görbítése határozza meg. Ezután a hüvelykujj a következő irányába mutat
Hogyan találja meg a bemeneti kimeneti szabályt?
A táblázatban szereplő minden számpárt ugyanaz a függvényszabály kapcsolja össze. Ez a szabály: szorozzon meg minden bemeneti számot (pl.{align*}xend{align*}-érték) 3-mal, hogy megtalálja az egyes kimeneti számokat (pl.{align*}yend{align*}-érték). Egy ehhez hasonló szabályt használhat más értékek keresésére is ehhez a függvényhez
Hogyan alakíthatja át a hányados szabályt szorzatszabálysá?
A hányados szabályt a termék- és láncszabályok alkalmazásának tekinthetjük. Ha Q(x) = f(x)/g(x), akkor Q(x) = f(x) * 1/(g(x)). Használhatja a szorzatszabályt a Q(x) megkülönböztetésére, az 1/(g(x)) pedig láncszabállyal, ahol u = g(x), és 1/(g(x)) = 1/u