Tartalomjegyzék:
Videó: Hogyan lehet bizonyítani egy sárkányt a koordináta geometriában?
2024 Szerző: Miles Stephen | [email protected]. Utoljára módosítva: 2023-12-15 23:37
Íme a két módszer:
- Ha egy négyszög két diszjunkt oldalpárja egybevágó, akkor ez egy sárkány (a hátoldala sárkány meghatározás).
- Ha egy négyszög egyik átlója a másik felező merőleges, akkor ez egy sárkány (egy tulajdonság megfordítása).
Ezt követően az is felmerülhet, hogy mik a sárkány tulajdonságai?
Sárkány A tulajdonságok közé tartozik (1) két pár egymást követő, egybevágó oldal, (2) egybevágó nem csúcsszögek és (3) merőleges átlók. További fontos sokszögtulajdonságok, amelyeket ismerni kell, a trapéz tulajdonságok, a paralelogramma tulajdonságok, a rombusz tulajdonságai, valamint a téglalap és négyzet tulajdonságai.
Tudja azt is, hogy a téglalap merőleges? Amint a bal oldali képeken látható, az a téglalap ne metsszék egymást derékszögben (nem merőleges ). (Hacsak nem a téglalap egy négyzet.) A metszéspont által alkotott szögek pedig nem mindig azonos mértékûek (nagyságúak). A szemben lévő középső szögek azonos méretűek (egybevágóak.)
Ezt követően a kérdés az, hogy a sárkány merőleges-e?
DEFINÍCIÓ: A sárkány olyan négyszög, amelynek négy oldala úgy van megrajzolva, hogy két különálló halmaza szomszédos, egybevágó oldalain. TÉTEL: Ha négyszög egy sárkány , az átlók merőleges . TÉTEL: Ha négyszög egy sárkány , van egy pár ellentétes szöge egybevágó.
A téglalap paralelogramma?
A téglalap két pár egymással párhuzamos oldala és négy derékszöge van. Ez is a paralelogramma , mivel két pár párhuzamos oldala van.
Ajánlott:
Hogyan találja meg az előképet a geometriában?
A T(V) kép a {k | halmazként van definiálva k=T(v) néhány v esetén V}-ben. Tehát x=T(y), ahol y a T^-1(S) eleme. S előképe az {m | halmaz T(m) S}-ben van. Így T(y) S-ben van, tehát mivel x=T(y), azt kapjuk, hogy x S-ben van
Lehet-e párhuzamos egy negatív és egy pozitív meredekség?
104. Tétel: Ha két egyenesnek azonos a meredeksége, akkor az egyenesek nem függőleges párhuzamos egyenesek. Ha két egyenes merőleges, és egyik sem függőleges, akkor az egyik egyenes pozitív, a másik negatív meredekségű. Ezenkívül a meredekségük abszolút értéke reciprok
Mi a 4 kvadráns egy koordináta gráfon?
Az egymást metsző x- és y-tengelyek négy szakaszra osztják a koordinátasíkot. Ezt a négy szakaszt kvadránsoknak nevezzük. A kvadránsok elnevezése az I, II, III és IV római számokkal történik, a jobb felső negyedtől kezdődően az óramutató járásával ellentétes irányban haladva
Hogyan jelöli meg a pontokat a geometriában?
A pont a legalapvetőbb objektum geometria. Ezt egy pont jelöli, és a neve nagybetűvel történik. Egy pont csak pozíciót jelöl; nulla a mérete (azaz nulla hossza, nulla szélessége és nulla magassága). Az 1. ábra a C, M és Q pontot szemlélteti
Hogyan készítsünk koordinátasíkot a geometriában?
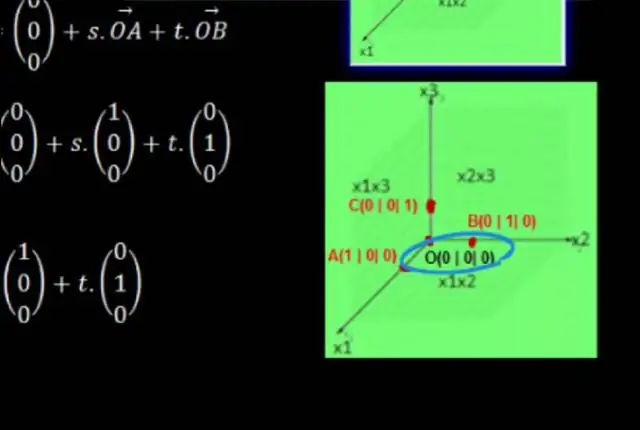
Koordinátasík létrehozásához a következő lépéseket hajtjuk végre: Rajzoljunk két egymásra merőleges számegyenest, amelyek mindkét egyenesen a 0 pontban metszik egymást. Jelölje be a vízszintes számegyenest x tengelynek, a függőleges számegyenest pedig y tengelynek