Videó: Mi az identitástörvény a diszkrét matematikában?
2024 Szerző: Miles Stephen | [email protected]. Utoljára módosítva: 2023-12-15 23:37
Így a azonosságtörvény , p∧T≡p, azt jelenti, hogy bármely p mondat és tetszőleges T tautológiájú kötőszó mindig ugyanazt az igazságértéket fogja bírni, mint p (azaz logikailag ekvivalens p-vel). Ez azt jelenti, hogy bármely p mondat diszjunkciója tetszőleges T tautológiával mindig igaz (maga is tautológia lesz).
Azt is tudni kell, hogy mi az azonosságtörvény a matematikában?
An identitás egy egyenlőség, amely a változóihoz választott értékektől függetlenül igaz. Például a identitás (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 minden választásra igaz x és y, függetlenül attól, hogy valós vagy komplex számokról van szó.
Továbbá, mi az azonosság elvének példája? A logikában a törvénye identitás kimondja, hogy minden dolog azonos önmagával. Ez az első a gondolkodás három törvénye közül, az ellentmondásmentesség és a kizárt közép törvénye mellett. Kevésbé formálisan is írható úgy, hogy A az A. Egy ilyen a elv a "Rose is a rose is a rose is a rose."
Ezt követően az is felmerülhet, hogy mi a De Morgan törvény a diszkrét matematikában?
De Morgan törvényei írja le, hogyan matematikai az állítások és fogalmak ellentétükön keresztül kapcsolódnak egymáshoz. A halmazelméletben De Morgan törvényei a halmazok metszéspontját és egyesülését komplementereken keresztül kapcsolják össze. A propozíciós logikában De Morgan törvényei a kijelentések kötő- és diszjunkcióit tagadással kapcsolja össze.
Mik azok a diszkrét matematikai vonatkozások?
Definíció: Legyenek p és q propozíciók. A p ∨ q-vel jelölt "p vagy q" állítás hamis, ha p és q is hamis, egyébként igaz. A p → q-vel jelölt "p q-t feltételezi" állítást nevezzük következmény . Hamis, ha p igaz, q pedig hamis, egyébként igaz.
Ajánlott:
Mit jelent a diszkrét szerkezet?
Diszkrét struktúra Diszkrét elemek halmaza, amelyen bizonyos műveleteket definiálnak. A diszkrét nem folytonos, ezért a diszkrét halmazok tartalmaznak véges és megszámlálható halmazokat, de nem megszámlálható halmazokat, például valós számokat
Mit jelent a mátrix a diszkrét matematikában?
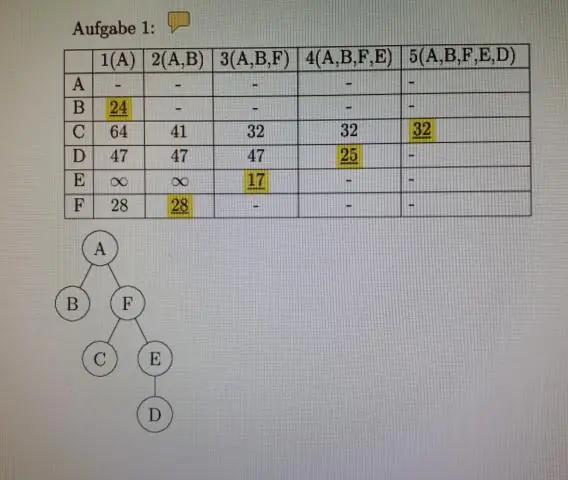
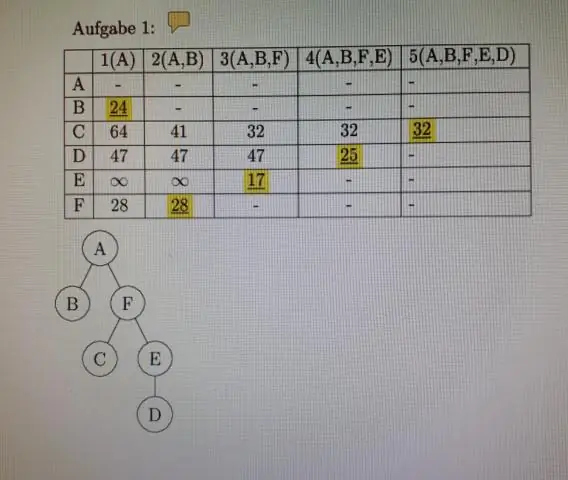
A diszkrét matematika és alkalmazásai 2. fejezet Megjegyzések 2.6 Mátrixok Előadásdiák Írta: Adil Aslammailto:[email protected]. A mátrix definíciója •A mátrix egy téglalap alakú számtömb. Az m sorból és n oszlopból álló mátrixot m x n mátrixnak nevezzük. A mátrix többes száma a mátrixok
Mi a diszkrét és a folyamatos a statisztikában?
Folyamatos vs. diszkrét elosztások. Vezérlődiagramok: A diszkrét eloszlás olyan, amelyben az adatok csak bizonyos értékeket, például egész számokat vehetnek fel. A folytonos eloszlás olyan, amelyben az adatok bármely értéket felvehetnek egy meghatározott tartományon belül (amely lehet végtelen)
Hogyan találja meg a folyamatos és diszkrét adatokat?
Egyszerűen fogalmazva, diszkrét adatokat számolunk, és folyamatos adatokat mérünk. A diszkrét adatok például a kutyák száma, a tanulók száma vagy a pénzösszeg. A folyamatos adat lehet a kutyák magassága vagy súlya, vagy egy mérföld lefutásához szükséges idő
Mi az ekvivalencia a diszkrét matematikában?
A matematikában az ekvivalenciareláció egy bináris reláció, amely reflexív, szimmetrikus és tranzitív. Az „egyenlő” reláció az ekvivalencia reláció kanonikus példája, ahol bármely a, b és c objektumra: a = a (reflexív tulajdonság), ha a = b és b = c, akkor a = c (tranzitív tulajdonság) )