Videó: Hogyan találja meg a trig függvény második deriváltját?
2024 Szerző: Miles Stephen | [email protected]. Utoljára módosítva: 2023-12-15 23:37
VIDEÓ
Csak hát, mik a 6 trig függvény származékai?
Trigonometrikus függvények származékai. Az alapvető trigonometrikus függvények a következő 6 függvényt tartalmazzák: szinusz ( bűn x), koszinusz ( kötözősaláta x), érintő (tanx), kotangens (cotx), szekáns (secx) és koszekáns (cscx). Mindezek a függvények folyamatosak és tartományukban differenciálhatók.
Ezt követően a kérdés az, hogy mi az 1 deriváltja? Az Derivált megmondja egy függvény bármely pontban mért meredekségét. Vannak szabályok, amelyeket követve sok mindent megtalálhatunk származékai . Például: Egy állandó érték meredeksége (például 3) mindig 0.
Derivált Szabályok.
| Közös funkciók | Funkció | Derivált |
|---|---|---|
| Állandó | c | 0 |
| Vonal | x | 1 |
| fejsze | a | |
| Négyzet | x2 | 2x |
Az emberek azt is kérdezik, hogy mi a COSX 27. származéka?
bűn
Mi az a cos 2x?
kötözősaláta ( 2x ) = kötözősaláta (x + x) = kötözősaláta (x) kötözősaláta (x) - sin(x)sin(x) = kötözősaláta ^ 2(x ) - bűn^ 2(x ) Tekintettel a Pythagore-i identitásokra: (sin^ 2(x ) + kötözősaláta ^ 2(x ) = 1), kötözősaláta ^ 2(x ) = 1 - sin^ 2(x ) így kötözősaláta ( 2x ) is egyenlő (1 - sin^ 2(x )) - bűn^ 2(x ) vagy 1 - 2sin^ 2(x )
Ajánlott:
Honnan tudod, hogy egy függvény nem függvény?
A függőleges vonal teszt segítségével viszonylag egyszerű meghatározni, hogy egy reláció függvény-e egy grafikonon. Ha egy függőleges vonal minden helyen csak egyszer metszi a relációt a grafikonon, akkor a reláció függvény. Ha azonban egy függőleges vonal többször keresztezi a relációt, akkor a reláció nem függvény
Hogyan találja meg a másodfokú függvény szimbolikus ábrázolását?
A másodfokú függvények szimbolikusan ábrázolhatók az y(x) = ax2 + bx + c egyenlettel, ahol a, b és c állandók, és a ≠ 0. Ezt az űrlapot szabványos űrlapnak nevezzük
Hogyan találja meg a másodfokú függvény maximális értékét?
Ha megadja az y = ax2 + bx + c képletet, akkor a maximális értéket a max =c- (b2 / 4a) képlet segítségével találhatja meg. Ha megvan az y = a(x-h)2 + k egyenlet, és a színház negatív, akkor a maximális érték k
Hogyan találja meg egy algebrai függvény tartományát?
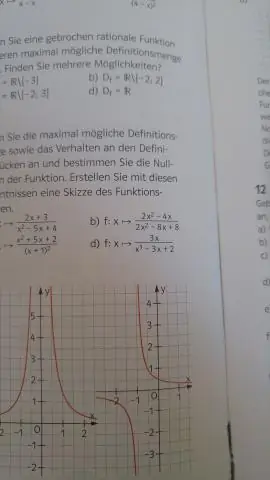
Egy függvény tartománya a függvény összes lehetséges bemenetének halmaza. Például az f(x)=x² tartomány minden valós szám, és a g(x)=1/x tartomány minden valós szám, kivéve x=0
Hogyan mutatja meg Newton második törvényét?
Newton második mozgástörvénye formálisan a következőképpen mondható ki: Egy tárgy nettó erő által keltett gyorsulása egyenesen arányos a nettó erő nagyságával, ugyanabban az irányban, mint a nettó erő, és fordítottan arányos a nettó erővel. a tárgy