Tartalomjegyzék:
Videó: Hogyan oldja meg az egyenlőség összeadási tulajdonságát?
2024 Szerző: Miles Stephen | [email protected]. Utoljára módosítva: 2023-12-15 23:37
Az egyenlőség kiegészítése
Ha két kifejezés egyenlő egymással, és az egyenlet mindkét oldalához ugyanazt az értéket adjuk, az egyenlet egyenlő marad. Amikor te megoldani egy egyenlet, akkor megtalálja annak a változónak az értékét, amely az egyenletet igazzá teszi. Azért, hogy megoldani az egyenlet, akkor izolálja a változót.
Ennek megfelelően mit jelent az egyenlőség összeadási tulajdonsága?
Az egyenlőség kiegészítése . Az ingatlan Ez azt jelenti, hogy ha egy egyenlet mindkét oldalához ugyanazt a számot adjuk, az oldalak egyenlők maradnak (azaz az egyenlet továbbra is igaz.)
Továbbá, melyik állítás a példa az egyenlőség összeadási tulajdonságára? Az az egyenlőség additív tulajdonsága kimondja, hogy ha egy egyenlet mindkét oldalához ugyanannyit adunk, akkor a egyenlőség még mindig igaz. Legyenek a, b és c valós számok, amelyek racionális számokból (pl. 0, -7 és 2/3) és irracionális számokból (pl. pi és 5 négyzetgyöke) állnak.
Hasonlóképpen felteszik a kérdést, hogyan oldják meg az egyenlőséget?
Összegzés
- Sok egyszerű egyenlőtlenség megoldható úgy, hogy mindkét oldalt összeadjuk, kivonjuk, szorozzuk vagy osztjuk, amíg a változó önmagában nem marad.
- De ezek a dolgok megváltoztatják az egyenlőtlenség irányát:
- Ne szorozzon vagy osszon változóval (hacsak nem tudja, hogy mindig pozitív vagy negatív)
Mi az egyenlőség 4 tulajdonsága?
- A reflexív tulajdonság. a =a.
- A szimmetrikus tulajdonság. Ha a=b, akkor b=a.
- A tranzitív ingatlan. Ha a=b és b=c, akkor a=c.
- A helyettesítő tulajdonság. Ha a=b, akkor a bármely egyenletben helyettesíthető b-vel.
- Az összeadás és kivonás tulajdonságai.
- A szorzási tulajdonságok.
- Az osztály tulajdonságai.
- A Square Roots ingatlan*
Ajánlott:
Hogyan oldja meg a Hardy Weinberg-problémákat?
VIDEÓ Ezen kívül hogyan találja meg P-t és Q-t Hardy Weinbergben? Mivel p = 1 - q és q ismert, lehetséges kiszámítja p is. Tudva p és q , egyszerű dolog ezeket az értékeket a Hardy - Weinberg egyenlet (p² + 2pq + q² = 1). Ez megadja a populáción belül a kiválasztott tulajdonság mindhárom genotípusának előrejelzett gyakoriságát.
Hogyan oldja meg az ideális gáztörvényt?
Ideális gáz törvényi képlete Ideális gáztörvény képlete Kérdések: Válasz: A térfogat V = 890,0 ml, a hőmérséklet T = 21°C és a nyomás P = 750 Hgmm. PV = nRT. Válasz: A mólok száma n = 3,00 mol, a hőmérséklet T = 24°C és a nyomás P = 762,4 Hgmm. PV = nRT
Hogyan oldja meg a törtek szorzását és osztását?
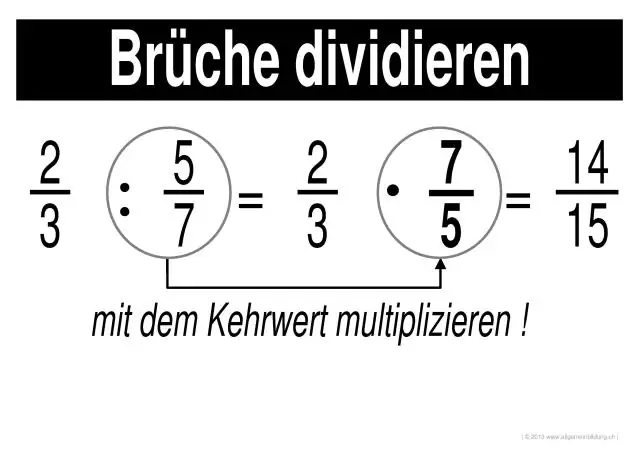
Törtek szorzása és osztása 1. lépés: Szorozzuk meg az egyes törtek számlálóit egymással (a felül lévő számokkal). Az eredmény a válasz számlálója. 2. lépés: Szorozzuk meg az egyes törtek nevezőit egymással (az alsó számok). Az eredmény a válasz nevezője. 3. lépés: Egyszerűsítse vagy csökkentse a választ
Hogyan oldja meg az identitástulajdonságot?
Az identitástulajdonság két részből áll: Additív identitás és Multiplikatív identitás. Adjunk hozzá nullát (0) egy számhoz, az összeg ez a szám. Szorozzuk meg a számot 1-gyel, a termék ez a szám. Ossz el egy számot önmagával, a hányados 1
Hogyan oldja meg grafikusan az LP-t Excelben?
VIDEÓ Ilyen módon hogyan lehet grafikusan megoldani egy problémát? Nak nek megoldani egy egyenlet azt jelenti, hogy megtaláljuk az összes értéket, amely igazzá teszi az állítást. Nak nek megoldani egy egyenlet grafikusan , rajzolja meg a grafikont az egyenlet minden oldalára, tagjára, és nézze meg, hogy a görbék hol egyenlők.