
- Szerző Miles Stephen [email protected].
- Public 2023-12-15 23:37.
- Utoljára módosítva 2025-01-22 16:59.
Tól től ebből következtethetünk arra, hogy:
Ha bármely két szám szorzata nulla, akkor az egyik vagy mindkét szám nulla. Vagyis ha ab = 0, akkor a = 0 vagy b = 0 (ami magában foglalja azt a lehetőséget, hogy a = b = 0). Ezt hívják a Null tényező törvény ; és mi használat gyakran arra másodfokú egyenleteket megoldani.
Hasonlóképpen felteszik a kérdést, hogy mi a 4 módja a másodfokú egyenlet megoldásának?
A négy másodfokú egyenlet megoldási módszerei faktorálást végeznek a négyzetgyök használatával, kiegészítik a négyzetet és a négyzetes képlet. Tehát amiről most beszélni szeretnék, az az összes különböző áttekintése másodfokú egyenlet megoldási módjai.
Továbbá mit jelent a négyzet befejezése? A tér befejezése másodfokú egyenlet megoldására szolgáló módszer az egyenlet alakjának megváltoztatásával úgy, hogy a bal oldal tökéletes legyen négyzet háromtagú. Az ax2+bx+c=0 megoldásához a négyzet befejezése : 1. Alakítsa át az egyenletet úgy, hogy a c konstans tag egyedül legyen a jobb oldalon.
Ezenkívül mi az a nullfaktor?
Az Null tényező Törvény Ha bármely két szám szorzata nulla, akkor az egyik vagy mindkét szám nulla. Vagyis ha ab = 0, akkor a = 0 vagy b = 0 (ami magában foglalja annak lehetőségét, hogy a = b = 0). Ezt hívják a Null tényező Törvény; és gyakran használjuk másodfokú egyenletek megoldására.
Mi a másodfokú egyenlet a matematikában?
A másodfokú egyenlet egy egyenlet másodfokú, ami azt jelenti, hogy legalább egy négyzetes tagot tartalmaz. A szabványos forma ax² + bx + c = 0, ahol a, b és c konstansok vagy numerikus együtthatók, x pedig ismeretlen változó.
Ajánlott:
Hogyan lehet algebrailag megoldani egy abszolút értékű egyenletet?

ABSZOLÚT ÉRTÉK(EK)ET TARTALMAZÓ EGYENLETEK MEGOLDÁSA 1. lépés: Különítse el az abszolút érték kifejezést. 2. lépés: Állítsa be az abszolút érték jelölésen belüli mennyiséget + és - az egyenlet másik oldalán lévő mennyiséggel. 3. lépés: Oldja meg az ismeretlent mindkét egyenletben. 4. lépés: Ellenőrizze válaszát analitikusan vagy grafikusan
Hogyan lehet megoldani egy egyenletet a változó elkülönítésével?
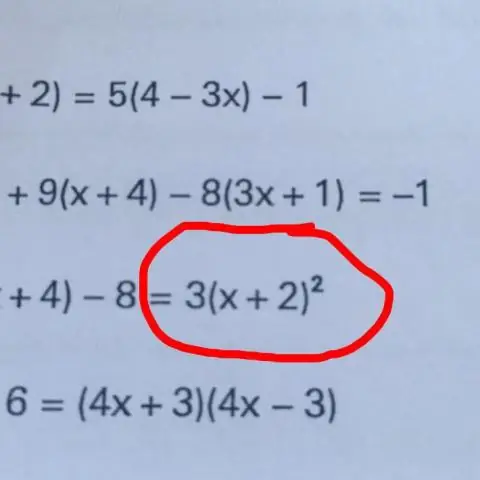
A változó elkülönítésének alapvető technikája az, hogy az egyenlet mindkét oldalával „tegyünk valamit”, például összeadjuk, kivonjuk, szorozzuk vagy elosztjuk az egyenlet mindkét oldalát ugyanazzal a számmal. Ezt a folyamatot megismételve megkaphatjuk az egyenlet egyik oldalán izolált változót
Hogyan lehet meghatározni egy piramis felületét háló segítségével?

VIDEÓ Ezzel kapcsolatban mekkora egy piramis teljes felülete? Az Piramis felülete Ha minden oldallap egyforma: [Alap Terület ] + 1 / 2 × Kerület × [ferde hossz] Az is felmerülhet, hogy hogyan lehet megtalálni a gömb felületét? Megtalálni a felszíni terület a szféra , használja a 4πr2 egyenletet, ahol r a sugarat jelöli, amelyet önmagával megszorozva négyzetre emeli.
Hogyan lehet átalakítani egy másodfokú egyenletet általános formáról szabványos formára?

Bármely másodfokú függvény felírható f(x) = a(x - h) 2 + k szabványos formában, ahol h és k az a, b és c együtthatóval vannak megadva. Kezdjük a másodfokú függvénnyel általános formában, és fejezzük be a négyzetet, hogy átírjuk szabványos alakba
Hogyan lehet megoldani egy lineáris egyenletet Gauss-eliminációval?

A Gauss-elimináció használata egyenletrendszerek megoldására Bármely sort megszorozhat egy konstanssal (a nullától eltérő). megszorozza a harmadik sort –2-vel, így új harmadik sort kap. Bármelyik két sort válthat. felcseréli az első és a második sort. Hozzáadhat két sort együtt. hozzáadja az első és a második sort, és beírja a második sorba
