Tartalomjegyzék:
Videó: Hogyan lehet megoldani egy lineáris egyenletet Gauss-eliminációval?
2024 Szerző: Miles Stephen | [email protected]. Utoljára módosítva: 2023-12-15 23:37
A Gauss-elimináció használata egyenletrendszerek megoldására
- Bármelyik sort megszorozhatja által egy állandó (nullától eltérő). megszorozza a harmadik sort által –2, hogy új hármas sort kapjon.
- Bármelyik két sort válthat. felcseréli az első és a második sort.
- Hozzáadhat két sort együtt. hozzáadja az első és a második sort, és megírja ban ben második sor.
Akkor hogyan működik a Gauss-elimináció?
Lazán szólva, Gauss eliminációs munkák felülről lefelé, hogy mátrixot hozzon létre lépcsőzetes formában, míg Gauss -Jordánia megszüntetése hol folytatódik Gauss-féle le kell hagyni, majd alulról felfelé dolgozva mátrixot hozunk létre redukált echelon formában. A technikát a következő példa szemlélteti.
Továbbá, mik a Cramer-szabálymátrixok? Cramer szabálya 2×2 rendszerhez (két változóval) Cramer szabálya egy másik módszer, amely determinánsok segítségével képes lineáris egyenletrendszereket megoldani. A jelölések tekintetében a mátrix szögletes zárójelbe zárt számokból álló tömb, míg döntő két függőleges sávval körülvett számok tömbje.
Másodszor, mi a Gauss-elimináció célja?
Gauss elimináció . A Wikipédiából, a szabad enciklopédiából. Gauss elimináció , más néven sorredukció, egy algoritmus a lineáris algebrában lineáris egyenletrendszer megoldására. Általában a megfelelő együtthatómátrixon végrehajtott műveletek sorozatát értjük.
Mi a különbség a Gauss és a Gauss Jordan elimináció között?
3 válasz. Gauss elimináció segít egy mátrixot sorlépcsős formába helyezni, míg Gauss - Jordan kiesés egy mátrixot csökkentett soros echelon formába helyez. Kis rendszerek esetén (vagy kézzel) általában kényelmesebb a használata Gauss - Jordan kiesése és explicit módon oldja meg az egyes reprezentált változókat ban,-ben mátrix rendszer.
Ajánlott:
Hogyan lehet megoldani egy másodfokú egyenletet a nullfaktor törvény segítségével?
Ebből arra következtethetünk, hogy: Ha bármely két szám szorzata nulla, akkor az egyik vagy mindkét szám nulla. Vagyis ha ab = 0, akkor a = 0 vagy b = 0 (ami magában foglalja azt a lehetőséget, hogy a = b = 0). Ezt nulltényezős törvénynek nevezik; és gyakran használjuk másodfokú egyenletek megoldására
Hogyan lehet grafikusan megoldani egy lineáris egyenletrendszert?
Egy lineáris egyenletrendszer grafikus megoldásához mindkét egyenletet ugyanabban a koordinátarendszerben ábrázoljuk. A rendszer megoldása a két egyenes metszéspontjában lesz. A két egyenes metszi egymást (-3, -4), ami ennek az egyenletrendszernek a megoldása
Hogyan lehet algebrailag megoldani egy abszolút értékű egyenletet?
ABSZOLÚT ÉRTÉK(EK)ET TARTALMAZÓ EGYENLETEK MEGOLDÁSA 1. lépés: Különítse el az abszolút érték kifejezést. 2. lépés: Állítsa be az abszolút érték jelölésen belüli mennyiséget + és - az egyenlet másik oldalán lévő mennyiséggel. 3. lépés: Oldja meg az ismeretlent mindkét egyenletben. 4. lépés: Ellenőrizze válaszát analitikusan vagy grafikusan
Hogyan lehet megoldani egy egyenletet a változó elkülönítésével?
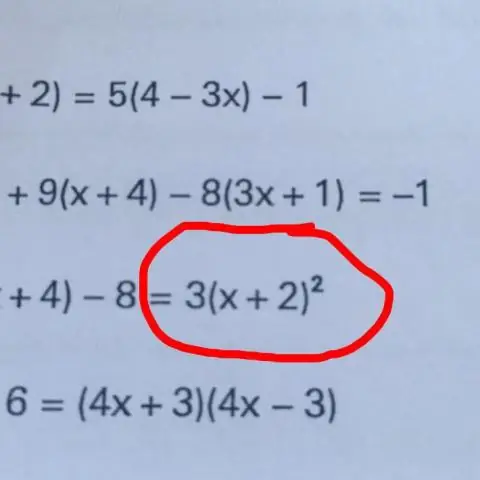
A változó elkülönítésének alapvető technikája az, hogy az egyenlet mindkét oldalával „tegyünk valamit”, például összeadjuk, kivonjuk, szorozzuk vagy elosztjuk az egyenlet mindkét oldalát ugyanazzal a számmal. Ezt a folyamatot megismételve megkaphatjuk az egyenlet egyik oldalán izolált változót
Hogyan lehet egy lineáris egyenletrendszert algebrailag megoldani?
Az elimináció segítségével oldja meg a közös megoldást a két egyenletben: x + 3y = 4 és 2x + 5y = 5. x= –5, y= 3. Az első egyenlet minden tagját szorozza meg –2-vel (–2x – 6y = –8), majd add össze a két egyenletben szereplő tagokat. Most oldd meg az –y = –3-at y-ra, és kapod, hogy y = 3