Tartalomjegyzék:
Videó: Hogyan konvertálhat másodfokú egyenletet csúcsformából számológéppé?
2024 Szerző: Miles Stephen | [email protected]. Utoljára módosítva: 2023-12-15 23:37
Számológép az alapformából a csúcsformába való konverzióhoz
- y=x2+3x+5.
- x2+3x+5=
- || +(p2)2-(p2)2=0.
- || a2+2ab+b2=(a+b)2.
- || -1⋅-1=+1.
- xS=-32=-1,5.
- yS=-(32)2+5=2,75.
Akkor hogyan lehet egy másodfokú egyenletet csúcsformává alakítani?
Nak nek alakítani a négyzetes y-ból = ax2 + bx + c forma nak nek csúcsforma , y = a(x - h)2+ k, a négyzet kitöltésének folyamatát használod. Lássunk egy példát. Alakítani y = 2x2 - 4x + 5 be csúcsforma , és adja meg a csúcs . Egyenlet y = ax2 + bx + c forma.
A fentieken kívül mi az a faktoros forma? A faktoros forma egy zárójeles algebrai kifejezés. Gyakorlatilag a faktoros forma szorzatok szorzata … vagy összegek szorzatainak összege… Bármely logikai függvény reprezentálható egy faktoros forma , és bármilyen faktoros forma valamilyen logikai függvény reprezentációja.
Ebben a tekintetben mi az egyenlet a csúcs megtalálásához?
A paraboláknak mindig van egy legalacsonyabb pontjuk (vagy a legmagasabb pontjuk, ha a parabola fejjel lefelé van). Ezt a pontot, ahol a parabola irányt változtat, " csúcs ". Ha a másodfokút y = a(x – h) alakban írjuk fel2 + k, majd a csúcs a pont (h, k).
Mi a parabola csúcsa?
Az Parabola csúcsa . Az parabola csúcsa az a pont, ahol a parabola keresztezi szimmetriatengelyét. Ha az x2 tag együtthatója pozitív, a csúcs a grafikon legalacsonyabb pontja lesz, az „U” alakzat alján található pont.
Ajánlott:
Hogyan lehet megoldani egy másodfokú egyenletet a nullfaktor törvény segítségével?
Ebből arra következtethetünk, hogy: Ha bármely két szám szorzata nulla, akkor az egyik vagy mindkét szám nulla. Vagyis ha ab = 0, akkor a = 0 vagy b = 0 (ami magában foglalja azt a lehetőséget, hogy a = b = 0). Ezt nulltényezős törvénynek nevezik; és gyakran használjuk másodfokú egyenletek megoldására
Hogyan néz ki egy másodfokú egyenlet grafikonja?
A másodfokú függvény grafikonja egy U alakú görbe, az úgynevezett parabola. Megrajzolható az egyenlet megoldásainak ábrázolásával, a csúcs megtalálásával és a szimmetriatengely segítségével a kiválasztott pontok ábrázolásával, vagy a gyökök és a csúcsok megkeresésével. A másodfokú egyenlet szabványos formája a
Hogyan találja meg a másodfokú függvény szimbolikus ábrázolását?
A másodfokú függvények szimbolikusan ábrázolhatók az y(x) = ax2 + bx + c egyenlettel, ahol a, b és c állandók, és a ≠ 0. Ezt az űrlapot szabványos űrlapnak nevezzük
Hogyan írjunk fel másodfokú egyenletet C++ nyelven?
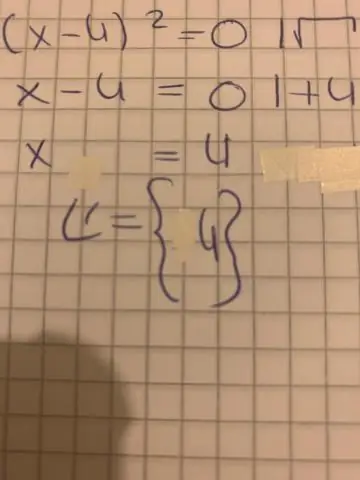
2. program: keresse meg a b-t és a c-t egy másodfokú egyenletben #include #include int main(){float a,b,c; float d,gyökér1,gyökér2; printf('Írja be a másodfokú egyenletet ax^2+bx+c formátumban: '); scanf('%fx^2%fx%f',&a,&b,&c); d = b*b-4*a*c;
Hogyan lehet átalakítani egy másodfokú egyenletet általános formáról szabványos formára?
Bármely másodfokú függvény felírható f(x) = a(x - h) 2 + k szabványos formában, ahol h és k az a, b és c együtthatóval vannak megadva. Kezdjük a másodfokú függvénnyel általános formában, és fejezzük be a négyzetet, hogy átírjuk szabványos alakba